A Deep Fourier Residual Method for solving PDEs using Neural Networks Jamie M. Taylor1 David Pardo234 and Ignacio Muga25
ADeepFourierResidualMethodforsolvingPDEsusingNeuralNetworksJamieM.Taylor1,DavidPardo2,3,4,andIgnacioMuga2,51DepartmentofQuantitativeMethods,CUNEFUniversity,Madrid,Spain2BasqueCenterforAppliedMathematics(BCAM),Bilbao,Bizkaia,Spain3UniversityoftheBasqueCountry(UPV/EHU),Leioa,Spain4Ikerbasque(BasqueFou...
相关推荐
-
公司日常考勤制度VIP免费

 2024-11-29 7
2024-11-29 7 -
公司人事考勤制度VIP免费

 2024-11-29 9
2024-11-29 9 -
公司规章制度汇编VIP免费

 2024-11-29 10
2024-11-29 10 -
岗位绩效工资制度VIP免费

 2024-11-29 10
2024-11-29 10 -
保密制度汇编VIP免费

 2024-11-29 11
2024-11-29 11 -
《绩效管理制度》VIP免费

 2024-11-29 12
2024-11-29 12 -
《施工企业安全生产评价标准》JGJ/T-77—2010VIP免费

 2024-12-14 178
2024-12-14 178 -
《潮起:中国创新型企业的诞生》导读VIP免费

 2024-12-14 59
2024-12-14 59 -
岗位面试题库合集-通用面试题库-世界五百强面试题目及应答评点(全套50题)VIP免费

 2024-12-15 67
2024-12-15 67 -
(试行)建设项目工程总承包合同示范文本GF-2011-0216VIP免费

 2025-01-13 132
2025-01-13 132
作者详情
相关内容
-

49_2019年离职面谈技巧大全
分类:人力资源/企业管理
时间:2025-08-23
标签:无
格式:DOC
价格:10 玖币
-
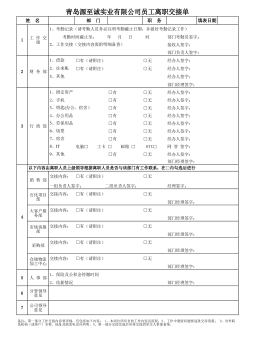
48_员工离职交接单
分类:人力资源/企业管理
时间:2025-08-23
标签:无
格式:XLS
价格:10 玖币
-
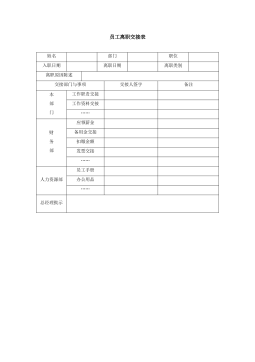
47_员工离职交接表-模板
分类:人力资源/企业管理
时间:2025-08-23
标签:无
格式:DOC
价格:10 玖币
-
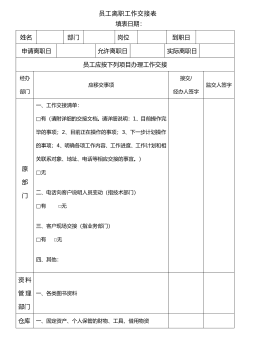
46_员工离职工作交接表
分类:人力资源/企业管理
时间:2025-08-23
标签:无
格式:DOC
价格:10 玖币
-
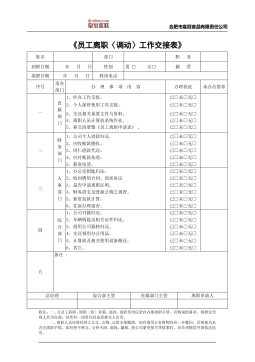
45_员工离职〈调动〉工作交接表
分类:人力资源/企业管理
时间:2025-08-23
标签:无
格式:DOC
价格:10 玖币



 渝公网安备50010702506394
渝公网安备50010702506394
