List homomorphisms by deleting edges and vertices tight complexity bounds for bounded-treewidth graphs Barış Can EsmerJacob FockeDániel MarxPaweł Rzążewski
Listhomomorphismsbydeletingedgesandvertices:tightcomplexityboundsforbounded-treewidthgraphsBarışCanEsmer∗JacobFocke∗DánielMarx∗PawełRzążewski†AbstractThegoalofthispaperistoinvestigateafamilyofoptimizationproblemsarisingfromlistho-momorphisms,andtounderstandwhatthebestpossiblealgorithmsareifwerestric...
相关推荐
-
【词汇变形总汇】2025高考词汇变形总汇 - 教师版VIP免费

 2024-12-06 5
2024-12-06 5 -
【超简37页】新课标高考英语考纲3500词汇VIP免费

 2024-12-06 16
2024-12-06 16 -
《高考英语3500词详解》(WORD版)VIP免费

 2024-12-06 30
2024-12-06 30 -
《高考英语3500词详解》VIP免费

 2024-12-06 27
2024-12-06 27 -
高中英语-[教师版]80天通关高考3500词汇VIP免费

 2024-12-06 33
2024-12-06 33 -
高中人教选修7课文逐句翻译VIP免费

 2024-12-06 14
2024-12-06 14 -
高中人教选修7课文原文及翻译VIP免费

 2024-12-06 38
2024-12-06 38 -
高中人教必修4课文逐句翻译VIP免费

 2024-12-06 20
2024-12-06 20 -
高中人教必修4课文原文及翻译VIP免费

 2024-12-06 53
2024-12-06 53 -
高考英语核心高频688词汇VIP免费
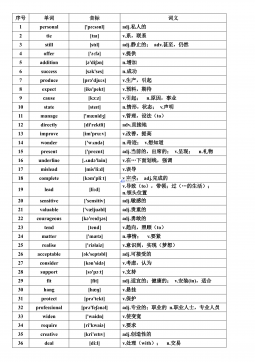
 2024-12-06 33
2024-12-06 33
作者详情
相关内容
-

江苏省南通市名校联盟2024—2025学年高三模拟演练语文
分类:中学教育
时间:2026-01-20
标签:无
格式:DOCX
价格:10 玖币
-

江苏省南通市海安市2024-2025学年高三上学期开学英语试题(无答案)
分类:中学教育
时间:2026-01-20
标签:无
格式:DOCX
价格:10 玖币
-

江苏省南通市海安市2024-2025学年高三上学期开学考试语文试题(无答案)
分类:中学教育
时间:2026-01-20
标签:无
格式:DOCX
价格:10 玖币
-

江苏省南京市、盐城市2025届高三上学期第一次模拟考试语文试题(含答案)
分类:中学教育
时间:2026-01-20
标签:无
格式:DOCX
价格:10 玖币
-

江苏省南京师范大学附属中学2025届高三上学期暑假测试物理试卷答案
分类:中学教育
时间:2026-01-20
标签:无
格式:DOCX
价格:10 玖币



 渝公网安备50010702506394
渝公网安备50010702506394
