第十三章 专题强化十四 应用气体实验定律解决“三类模型问题”
专题强化十四 应用气体实验定律解决“三类模型问题”专题解读1.本专题是气体实验定律在玻璃管液封模型、汽缸活塞类模型、变质量气体模型中的应用,高考在选考模块中通常以计算题的形式命题.2.学好本专题可以帮助同学们熟练的选取研究对象和状态变化过程,掌握处理三类模型问题的基本思路和方法.3.本专题用到的相关知识和方法有:受力分析、压强的求解方法、气体实验定律等.命题点一 “玻璃管液封”模型1.三大气体实验定律(1)玻意耳定律(等温变化):p1V1=p2V2或pV=C(常数).(2)查理定律(等容变化):=或=C(常数).(3)盖—吕萨克定律(等压变化):=或=C(常数).2.利用气体实验定律及气态方程...
相关推荐
-
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包05专题五 走进社会生活 遵守社会规则VIP免费

 2024-11-21 24
2024-11-21 24 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包05专题五 走进社会生活 遵守社会规则VIP免费

 2024-11-21 21
2024-11-21 21 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包03专题三 青春时光 做情绪情感的主人VIP免费

 2024-11-21 15
2024-11-21 15 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包03专题三 青春时光 做情绪情感的主人VIP免费

 2024-11-21 19
2024-11-21 19 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包02专题二 友谊的天空 师长情谊VIP免费

 2024-11-21 19
2024-11-21 19 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包02专题二 友谊的天空 师长情谊VIP免费

 2024-11-21 20
2024-11-21 20 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包01专题一 成长的节拍 生命的思考VIP免费

 2024-11-21 21
2024-11-21 21 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包01专题一 成长的节拍 生命的思考VIP免费

 2024-11-21 21
2024-11-21 21 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包《53中考》全国道德与法治资料包VIP免费

 2024-11-21 24
2024-11-21 24 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包07专题七 坚持宪法至上 崇尚法治精神VIP免费

 2024-11-21 18
2024-11-21 18
作者详情
相关内容
-

2025届重庆市西南大学附属中学高三下学期5月全镇模拟物理试题(含答案)
分类:中学教育
时间:2025-12-31
标签:无
格式:PDF
价格:10 玖币
-

2025届重庆市西南大学附属中学高三下学期5月全镇模拟化学试题(含答案)
分类:中学教育
时间:2025-12-31
标签:无
格式:PDF
价格:10 玖币
-
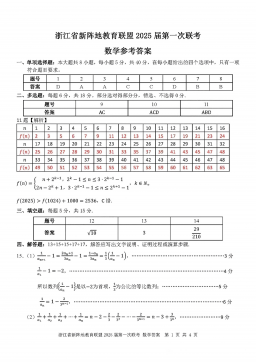
2025届浙江省新阵地联盟高三10月联考数学答案
分类:中学教育
时间:2025-12-31
标签:无
格式:PDF
价格:10 玖币
-

2025届重庆市西南大学附属中学高三下学期5月全镇模拟数学试题(含答案)
分类:中学教育
时间:2025-12-31
标签:无
格式:PDF
价格:10 玖币
-

2025届重庆康德三诊英语+答案
分类:中学教育
时间:2026-01-03
标签:无
格式:PDF
价格:10 玖币




 渝公网安备50010702506394
渝公网安备50010702506394
