六年级上册数学苏教版知识要点
一长方体和正方体一、长方体的认识1.认识长方体的面、棱、顶点。(1)从不同的角度观察同一个长方体。把长方体放在桌面上,无论从哪个角度观察,最多只...能同时观察到长方体的三个面。..............(2)长方体的棱和顶点。长方体两个面相交的线叫作长方体的棱,三条棱相交的点叫作长方体的顶点。2.长方体的特征。长方体是由6个长方形(也可能有2个相对的面是正方形)围成的立体图形,它有6个面、12条棱和8个顶点。在一个长方体中,相对的面完全相同,相对的棱长度相等。3.长方体长、宽、高的含义。长方体相交于同一顶点的三条棱的长度.................,.分别叫作....它的长、宽、高。...
相关推荐
-
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包05专题五 走进社会生活 遵守社会规则VIP免费

 2024-11-21 24
2024-11-21 24 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包05专题五 走进社会生活 遵守社会规则VIP免费

 2024-11-21 22
2024-11-21 22 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包03专题三 青春时光 做情绪情感的主人VIP免费

 2024-11-21 15
2024-11-21 15 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包03专题三 青春时光 做情绪情感的主人VIP免费

 2024-11-21 19
2024-11-21 19 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包02专题二 友谊的天空 师长情谊VIP免费

 2024-11-21 19
2024-11-21 19 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包02专题二 友谊的天空 师长情谊VIP免费

 2024-11-21 20
2024-11-21 20 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包01专题一 成长的节拍 生命的思考VIP免费

 2024-11-21 23
2024-11-21 23 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包01专题一 成长的节拍 生命的思考VIP免费

 2024-11-21 21
2024-11-21 21 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包《53中考》全国道德与法治资料包VIP免费

 2024-11-21 24
2024-11-21 24 -
曲一线系列初中《5中考3年模拟》2023专题解释全国道德与法治资料包07专题七 坚持宪法至上 崇尚法治精神VIP免费

 2024-11-21 18
2024-11-21 18
相关内容
-

2025届重庆市西南大学附属中学高三下学期5月全镇模拟物理试题(含答案)
分类:中学教育
时间:2025-12-31
标签:无
格式:PDF
价格:10 玖币
-

2025届重庆市西南大学附属中学高三下学期5月全镇模拟化学试题(含答案)
分类:中学教育
时间:2025-12-31
标签:无
格式:PDF
价格:10 玖币
-
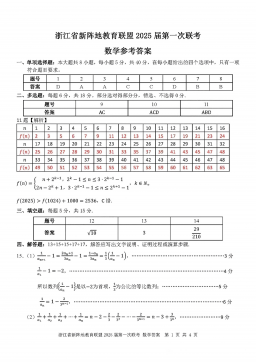
2025届浙江省新阵地联盟高三10月联考数学答案
分类:中学教育
时间:2025-12-31
标签:无
格式:PDF
价格:10 玖币
-

2025届重庆市西南大学附属中学高三下学期5月全镇模拟数学试题(含答案)
分类:中学教育
时间:2025-12-31
标签:无
格式:PDF
价格:10 玖币
-

2025届重庆康德三诊英语+答案
分类:中学教育
时间:2026-01-03
标签:无
格式:PDF
价格:10 玖币




 渝公网安备50010702506394
渝公网安备50010702506394
