2025年教学资料:3.3.2 函数的奇偶性(分层作业)(解析版)
3.3.2函数的奇偶性同步练习1.偶函数的图象关于轴对称,下列图象中,可以表示偶函数的是( ).A.B.C.D.【答案】A【分析】根据图像是否关于轴对称判断.【详解】A的图像关于轴对称,故A符合题意.BCD的图像都不关于轴对称,故BCD均不符合题意.故选:A.2.下列函数是偶函数的是( A )A.y=2x2-3 B.y=x3C.y=x2,x∈[0,1] D.y=x[解析] 对于A:f(-x)=2(-x)2-3=2x2-3=f(x),所以f(x)是偶函数,B,D都为奇函数,C中定义域不关于原点对称,函数不具备奇偶性.3.下列函数中,在其定义域内,既是奇函数又是减函数的是( ...
相关推荐
-
政治理论应知应会 100 题VIP免费

 2024-12-12 388
2024-12-12 388 -
2025年中央机关及其直属机构录用公务员考试 行政职业能力测验(地市级)(经典模考卷三)解析VIP免费

 2024-12-12 48
2024-12-12 48 -
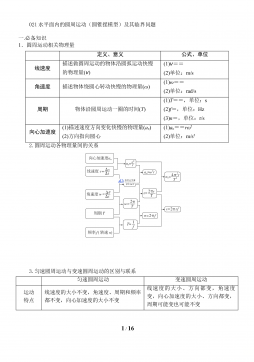
021水平面内的圆周运动(圆锥摆模型)及其临界问题 精讲精练-2022届高三物理一轮复习疑难突破微专题VIP免费
 2025-01-04 46
2025-01-04 46 -
21学位英语:从句考点真题VIP免费

 2025-04-08 7
2025-04-08 7 -
19学位英语:2010年阅读理解分析VIP免费

 2025-04-08 4
2025-04-08 4 -
[16] 学位英语:2007年阅读理解分析VIP免费

 2025-04-08 4
2025-04-08 4 -
[15] 学位英语:2006年阅读理解分析VIP免费

 2025-04-08 11
2025-04-08 11 -
[14] 学位英语:2005年阅读理解分析VIP免费

 2025-04-08 13
2025-04-08 13 -
[13] 学位英语:2004年阅读理解分析VIP免费

 2025-04-08 10
2025-04-08 10 -
[10] 学位英语:长难句拆分(二)VIP免费

 2025-04-08 11
2025-04-08 11
相关内容
-

[16] 学位英语:2007年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[15] 学位英语:2006年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[14] 学位英语:2005年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[13] 学位英语:2004年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[10] 学位英语:长难句拆分(二)
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币




 渝公网安备50010702506394
渝公网安备50010702506394
