2025年教学资料:3.3函数的性质
授课题目3.3函数的性质选用教材高等教育出版社《数学》(基础模块上册)授课时长4课时授课类型新授课教学提示本课将通过实例和学生熟悉的函数图像,帮助学生理解函数的单调性和奇偶性,引导学生正确地使用符号语言刻画函数的单调性和奇偶性,并通过几种常见函数:一次函数、反比例函数、二次函数整体系统地研究函数的性质.教学目标结合函数图像,能用数学语言表达函数单调性、奇偶性的定义,能通过图像法和定义法判断函数的单调性和奇偶性,逐步提高直观想象和数学抽象等核心素养;能利用函数的单调性判断同一单调区间内两个函数值的大小,知道函数奇偶性与函数图像对称性之间的关系,能从函数单调性、奇偶性等角度,重新认识一次函数、反比...
相关推荐
-
政治理论应知应会 100 题VIP免费

 2024-12-12 388
2024-12-12 388 -
2025年中央机关及其直属机构录用公务员考试 行政职业能力测验(地市级)(经典模考卷三)解析VIP免费

 2024-12-12 48
2024-12-12 48 -
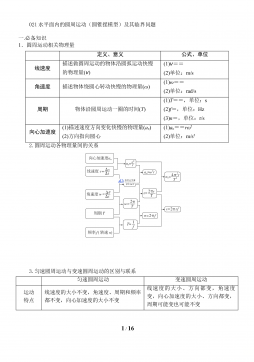
021水平面内的圆周运动(圆锥摆模型)及其临界问题 精讲精练-2022届高三物理一轮复习疑难突破微专题VIP免费
 2025-01-04 46
2025-01-04 46 -
21学位英语:从句考点真题VIP免费

 2025-04-08 7
2025-04-08 7 -
19学位英语:2010年阅读理解分析VIP免费

 2025-04-08 4
2025-04-08 4 -
[16] 学位英语:2007年阅读理解分析VIP免费

 2025-04-08 4
2025-04-08 4 -
[15] 学位英语:2006年阅读理解分析VIP免费

 2025-04-08 11
2025-04-08 11 -
[14] 学位英语:2005年阅读理解分析VIP免费

 2025-04-08 13
2025-04-08 13 -
[13] 学位英语:2004年阅读理解分析VIP免费

 2025-04-08 10
2025-04-08 10 -
[10] 学位英语:长难句拆分(二)VIP免费

 2025-04-08 11
2025-04-08 11
相关内容
-

[16] 学位英语:2007年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[15] 学位英语:2006年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[14] 学位英语:2005年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[13] 学位英语:2004年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[10] 学位英语:长难句拆分(二)
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币




 渝公网安备50010702506394
渝公网安备50010702506394
