
Path Association Rule Mining
Yuya Sasaki
sasaki@ist.osaka-u.ac.jp
Osaka University
ABSTRACT
Graph association rule mining is a data mining technique used for
discovering regularities in graph data. In this study, we propose
a novel concept, path association rule mining, to discover the cor-
relations of path patterns that frequently appear in a given graph.
Reachability path patterns (i.e., existence of paths from a vertex
to another vertex) are applied in our concept to discover diverse
regularities. We show that the problem is NP-hard, and we develop
an ecient algorithm in which the anti-monotonic property is used
on path patterns. Subsequently, we develop approximation and
parallelization techniques to eciently and scalably discover rules.
We use real-life graphs to experimentally verify the eectiveness
of path association rules and the eciency of our algorithm.
1 INTRODUCTION
Association rule mining is data mining technique used for dis-
covering regularities between itemsets in large databases [
1
,
49
].
Association rules are represented as
𝑋⇒𝑌
, where
𝑋
and
𝑌
are
the disjoint and called antecedent and consequent, respectively.
Association rules have attracted research attention because of their
usefulness in many applications such as market analysis [
27
], web
mining [29], and bioinformatics [32].
Regularities between entities in large-scale graphs are a critical
topic of research. Graph association rule mining on a single large
graph, which is an extended form of general association rule mining,
exhibits considerable potential for studying regularities [
14
,
18
,
19
,
45
]. Graph association rules are represented as
𝐺𝑋⇒𝐺𝑌
,
where
𝐺𝑋
and
𝐺𝑌
are graph patterns. Since graphs are widely
used in many applications, association rules on graphs have a large
opportunity to discovery valuable insights and knowledge.
Applications on graph association rule mining.
Graph associ-
ation rule mining exhibits numerous application scenarios.
Social analysis
: Social analysis is critical for understanding and im-
proving our life. Social relationships can be modeled using graphs,
and graph association rule mining can be used to discover regular-
ities between the status of people and their relationship patterns.
For example, social relationships aect to our health [
25
] and hap-
piness [
23
]. We can nd interesting rules, for example, “if people
are happy, they are healthy and have friends.”
Recommendation
: In current recommendation systems, user be-
havior, such as viewing and clicking [
11
,
31
], toward particular
products are tracked. Bipartite graphs are used to model user be-
havior to products. Graph association rule mining can be used nd
potential customers by nding regularities among user behavior,
products, and proles.
Social discrimination checking
: Social discrimination in graphs should
be solved for building fair machine learning models [
10
]. Machine
learning models for graph data can be suered from such discrimi-
natory bias as same as transactional data. Since graph association
rules can discover regularities that include discriminatory bias, they
can be used to remove discriminatory bias in the graph data.
Motivation and challenge.
Graph association rule mining is fun-
damental for graph analysis, but only a few techniques have been
developed [
14
,
18
,
19
,
45
]. Existing methods cannot be applied to
the aforementioned applications due to their own semantics (see
Sec. 7 in detail).
Existing works have four obstacles to apply the aforementioned
applications. First, in all existing works, a set of vertices in conse-
quent (i.e.,
𝐺𝑌
) must be a subset of those in the antecedent (i.e.,
𝐺𝑋
).
Thus, they cannot discover association rules such that
𝐺𝑋
and
𝐺𝑌
involve distinct vertices. Second, since
𝐺𝑋
and
𝐺𝑌
are restrictive
(e.g., a single edge or no common edges in
𝐺𝑋
and
𝐺𝑌
), they cannot
nd the dierence of vertex attributes. Third, each rule and discov-
ery algorithm assumes a single graph type, for example, graphs
with labeled vertices and unlabeled edges, and thus does not handle
more generalized graphs than that it assumes (e.g., if discovery
algorithms assume graphs with unlabeled edges, it cannot handle
ones with labeled edges). Fourth, their antecedent and consequent
are basic graph pattern, so it does not capture the connectivity
between vertices.
Therefore, we need a novel graph association rule mining tech-
nique. We introduce three challenges that have not been addressed
in existing studies. First, simple association rules are required to
exibly capture regularities that can represent (1) no restriction of
vertices in antecedent and consequent and (2) connectivity between
vertices. Second, an ecient and scalable mining algorithm is re-
quired to accurately nd all frequent patterns in general property
graphs that include vertex attributes and edge labels. Finally, such
rules should be eective and provide insight and knowledge, and
oer conventional metrics such as support, condence, and lift.
Contribution.
We propose a novel and simple concept, path as-
sociation rule mining, and develop an ecient and scalable algo-
rithm for discovering path association rules. Path association rule
mining aims to discover regularities between path patterns; path
patterns are sequences of vertex attribute sets and edge labels.
Reachablity patterns can be applied as path patterns that repre-
sent label-constrained reachability between two vertices in directed
edges. This mining nds rules
𝑝𝑋⇒𝑝𝑌
such that more than
𝜃
vertices become sources of path patterns
𝑝𝑋
and
𝑝𝑌
, where
𝜃
is
a given minimum support. This rule can naturally oer standard
metrics, such as absolute/relative support, condence, and lift.
Example 1.1. Figure 1 illustrates an example of path associa-
tion rule mining. A given graph includes 12 vertices, 15 edges, 4
types of edge labels, and 8 types of vertex attributes. From this
graph, we mine path association rules with
𝜃
is one. Path pattern
⟨{Male},Follows,{Art}⟩
is frequent because vertices
𝑣8
and
𝑣9
be-
come the sources of the path patterns (we say that
𝑣8
and
𝑣9
match
with the path pattern). Similarly, path pattern
⟨{CS},BelongTo,{Uni}⟩
arXiv:2210.13136v1 [cs.DB] 24 Oct 2022

 2024-12-10 12
2024-12-10 12
 2024-12-10 12
2024-12-10 12
 2024-12-10 12
2024-12-10 12
 2024-12-10 15
2024-12-10 15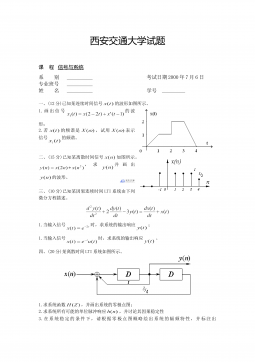
 2024-12-10 13
2024-12-10 13
 2024-12-10 15
2024-12-10 15
 2024-12-10 11
2024-12-10 11
 2024-12-10 18
2024-12-10 18
 2024-12-10 17
2024-12-10 17
 2024-12-10 12
2024-12-10 12








 渝公网安备50010702506394
渝公网安备50010702506394
