2025年中考数学专题复习:利用二次函数性质解决线段最值问题(含解析)
更多更新资料详情加微:xiaojuzi9598或zhixing16881利用二次函数性质解决线段最值问题方法突破练1.如图,已知抛物线y=x²+2x−3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,点M是线段AC下方抛物线上一点,过点M作y轴的平行线与AC交于点N,求线段MN的最大值.2.如图,已知抛物线y=−x²+2x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,点P是线段BC上方抛物线上一点,过点P作PM⊥BC于点M,求线段PM的最大值.3.如图,已知抛物线y=−x²+2x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,点...
相关推荐
-
公司日常考勤制度VIP免费

 2024-11-29 19
2024-11-29 19 -
公司人事考勤制度VIP免费

 2024-11-29 22
2024-11-29 22 -
公司规章制度汇编VIP免费

 2024-11-29 20
2024-11-29 20 -
岗位绩效工资制度VIP免费

 2024-11-29 22
2024-11-29 22 -
保密制度汇编VIP免费

 2024-11-29 22
2024-11-29 22 -
《绩效管理制度》VIP免费

 2024-11-29 24
2024-11-29 24 -
《施工企业安全生产评价标准》JGJ/T-77—2010VIP免费

 2024-12-14 263
2024-12-14 263 -
《潮起:中国创新型企业的诞生》导读VIP免费

 2024-12-14 74
2024-12-14 74 -
岗位面试题库合集-通用面试题库-世界五百强面试题目及应答评点(全套50题)VIP免费

 2024-12-15 81
2024-12-15 81 -
(试行)建设项目工程总承包合同示范文本GF-2011-0216VIP免费

 2025-01-13 148
2025-01-13 148
相关内容
-
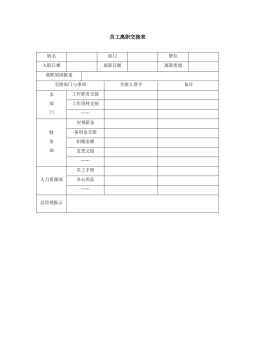
47_员工离职交接表-模板
分类:人力资源/企业管理
时间:2025-08-23
标签:无
格式:DOC
价格:10 玖币
-
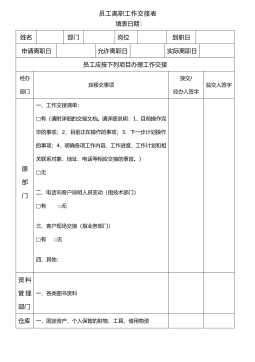
46_员工离职工作交接表
分类:人力资源/企业管理
时间:2025-08-23
标签:无
格式:DOC
价格:10 玖币
-
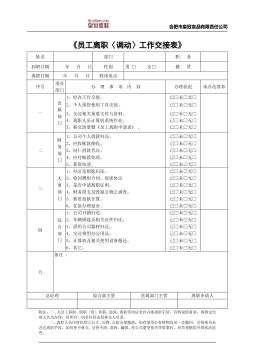
45_员工离职〈调动〉工作交接表
分类:人力资源/企业管理
时间:2025-08-23
标签:无
格式:DOC
价格:10 玖币
-

2025年行政事业性国有资产报告软件操作讲解20251216
分类:人力资源/企业管理
时间:2026-01-05
标签:无
格式:PPTX
价格:10 玖币
-

2025年度行政事业性国有资产报告 - 资产报告及公共基础设施等20251217
分类:人力资源/企业管理
时间:2026-01-05
标签:无
格式:PPTX
价格:10 玖币




 渝公网安备50010702506394
渝公网安备50010702506394
