The Complexity of Online Graph Games
TheComplexityofOnlineGraphGamesJanoschFuchsDepartmentofComputerScience,RWTHAachenUniversity,Germanyfuchs@algo.rwth-aachen.deChristophGrüneDepartmentofComputerScience,RWTHAachenUniversity,Germanygruene@algo.rwth-aachen.deTomJanßenDepartmentofComputerScience,RWTHAachenUniversity,Germanyjanssen@algo.rw...
相关推荐
-
2021 年全国硕士研究生入学统一考试英语(一)试题及参考答案VIP免费

 2024-12-02 4
2024-12-02 4 -
2016年一级注册消防工程师消防安全案例分析VIP免费

 2024-12-03 7
2024-12-03 7 -
2017年注册消防工程师案例分析真题解析VIP免费

 2024-12-03 4
2024-12-03 4 -
2015年注册消防工程师案例真题解析VIP免费
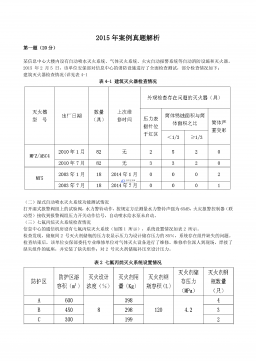
 2024-12-03 32
2024-12-03 32 -
2019年注册消防工程师案例分析真题解析VIP免费

 2024-12-03 34
2024-12-03 34 -
消防综合能力真题按章节版(2015-2019年)VIP免费

 2024-12-03 15
2024-12-03 15 -
消防技术实务真题按章节版(2015-2019)VIP免费

 2024-12-03 13
2024-12-03 13 -
2018年注册消防工程师案例分析真题解析VIP免费

 2024-12-03 23
2024-12-03 23 -
2006年中央、国家机关公务员录用考试行政职业能力测试真题及答案解析(A类)【完整+答案+解析】VIP免费

 2024-12-13 119
2024-12-13 119 -
2008年0706河南公务员考试《行测》真题VIP免费

 2025-02-25 9
2025-02-25 9
作者详情
相关内容
-

2007年天津市公务员考试《行测》真题(春季卷)答案及解析
分类:
时间:2025-02-07
标签:无
格式:PDF
价格:5.9 玖币
-

2005年江苏省公务员考试《行测》真题(B类卷)答案及解析
分类:
时间:2025-02-07
标签:无
格式:PDF
价格:5.9 玖币
-

2010年广东公务员考试《行测》真题(部分题目缺失)
分类:
时间:2025-02-25
标签:无
格式:PDF
价格:5.9 玖币
-

2010年北京公务员考试《行测》真题
分类:
时间:2025-02-25
标签:无
格式:PDF
价格:5.9 玖币
-

2008年0706河南公务员考试《行测》真题
分类:
时间:2025-02-25
标签:无
格式:PDF
价格:5.9 玖币



 渝公网安备50010702506394
渝公网安备50010702506394
