
Maximum Likelihood Learning of Unnormalized Models for Simulation-Based Inference
portant when comparing ABC to targeted SBI methods, im-
plemented in a multi-round procedure that refines the model
around the observed data, by sequentially simulating data
points that are closer to the observed ones (Greenberg et al.,
2019;Papamakarios et al.,2019;Hermans et al.,2020).
Previous model-based SBI methods have used their para-
metric estimator to learn the likelihood (e.g. the condi-
tional density specifying the probability of an observation
being simulated given a specific parameter set, Wood 2010;
Papamakarios et al. 2019;Pacchiardi & Dutta 2022), the
likelihood-to-marginal ratio (Hermans et al.,2020), or the
posterior function directly (Greenberg et al.,2019). We fo-
cus in this paper on likelihood-based (also called Synthetic
Likelihood; SL, in short) methods, of which two main in-
stances exist: (Sequential) Neural Likelihood Estimation
(or (S)NLE) (Papamakarios et al.,2019), which learns a
likelihood estimate using a normalizing flow trained by
optimizing a Maximum Likelihood (ML) loss; and Score
Matched Neural Likelihood Estimation (SMNLE Pacchiardi
& Dutta 2022), which learns an unnormalized (or Energy-
Based,LeCun et al. 2006) likelihood model trained using
conditional score matching. Recently, SNLE was applied
successfully to challenging neural data (Deistler et al.,2021).
However, limitations still remain in the approaches taken
by both (S)NLE and SMNLE. On the one hand, flow-based
models may need to use very complex architectures to prop-
erly approximate distributions with rich structure such as
multi-modality (Kong & Chaudhuri,2020;Cornish et al.,
2020). On the other hand, score matching, the objective of
SMNLE, minimizes the Fisher Divergence between the data
and the model, a divergence that fails to capture important
features of probability distributions such as mode propor-
tions (Wenliang & Kanagawa,2020;Zhang et al.,2022).
This is unlike Maximimum-Likelihood based-objectives,
whose maximizers satisfy attractive theoretical properties
(Bickel & Doksum,2015).
Contributions.
In this work, we introduce Amortized Un-
normalized Likelihood Neural Estimation (AUNLE), and Se-
quential UNLE, a pair of SBI Synthetic Likelihood methods
performing respectively sequential and targeted inference.
Both methods learn a Conditional Energy Based Model of
the simulator’s likelihood using a Maximum Likelihood
(ML) objective, and perform MCMC on the posterior esti-
mate obtained after invoking Bayes’ Rule. While posteriors
arising from conditional EBMs exhibit a particular form of
intractability called double intractability, which requires the
use of tailored MCMC techniques for inference, we train
AUNLE using a new approach which we call tilting. This
approach automatically removes this intractability in the
final posterior estimate, making AUNLE compatible with
standard MCMC methods, and significantly reducing the
computational burden of inference. Our second method,
SUNLE, departs from AUNLE by using a new training
technique for conditional EBMs which is suited when the
proposal distribution is not analytically available. While
SUNLE returns a doubly intractable posterior, we show that
inference can be carried out accurately through robust im-
plementations of doubly-intractable MCMC or variational
methods. We demonstrate the properties of AUNLE and
SUNLE on an array of synthetic benchmark models (Lueck-
mann et al.,2021), and apply SUNLE to a neuroscience
model of the crab Cancer borealis, where we improve the
posterior accuracy over prior state-of-the-art while need-
ing only a fraction of the simulations required by the most
efficient previous method (Gl¨
ockler et al.,2021).
Figure 1.
Performance of SMNLE, NLE and AUNLE, all trained
using a simulator with a bimodal likelihood
p(x|θ)
and a Gaussian
prior
p(θ)
, using 1000 samples. Top: simulator likelihood
p(x|θ0)
for some fixed θ0. Bottom: posterior estimate.
2. Background
Simulation Based Inference (SBI) refers to the set of meth-
ods aimed at estimating the posterior
p(θ|xo)
of some un-
observed parameters
θ∈Θ⊂RdΘ
given some observed
variable
xo∈ X ⊂ RdX
recorded from a physical system,
and a prior
p(θ)
. In SBI, one assumes access to a simula-
tor
G: (θ, u)7−→ y=G(θ, u)
, from which samples
y|θ
can be drawn, and whose associated likelihood
p(y|θ)
accu-
rately matches the likelihood
p(x|θ)
of the physical system
of interest. Here,
u
represents draws of all random variables
involved in performing draws of
x|θ
. By a slight abuse of
notation, we will not distinguish between the physical ran-
dom variable
x
representing data from the physical system
of interest, and the simulated random variable
y
drawn from
the simulator: we will use
x
for both. The complexity of the

 2024-12-01 6
2024-12-01 6
 2024-12-01 4
2024-12-01 4
 2024-12-01 4
2024-12-01 4
 2024-12-01 4
2024-12-01 4
 2024-12-01 8
2024-12-01 8
 2024-12-01 30
2024-12-01 30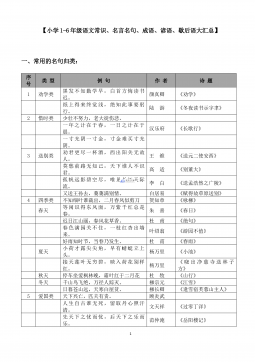
 2024-12-01 23
2024-12-01 23
 2024-12-01 17
2024-12-01 17
 2024-12-01 9
2024-12-01 9
 2024-12-01 13
2024-12-01 13







 渝公网安备50010702506394
渝公网安备50010702506394
