LECLERCS CONJECTURE ON A CLUSTER STRUCTURE FOR TYPE A RICHARDSON VARIETIES KHRYSTYNA SERHIYENKO AND MELISSA SHERMAN-BENNETT
LECLERC'SCONJECTUREONACLUSTERSTRUCTUREFORTYPEARICHARDSONVARIETIESKHRYSTYNASERHIYENKOANDMELISSASHERMAN-BENNETTAbstract.Leclerc[Lec16]constructedaconjecturalclusterstructureonRichardsonvarietiesinsimplylacedtypesusingclustercategories.WeshowthatintypeA,hisconjecturalclusterstructureisinfactaclusterstr...
相关推荐
-
小学生交通安全常识VIP免费

 2024-12-01 6
2024-12-01 6 -
小学生公共场所礼仪VIP免费

 2024-12-01 4
2024-12-01 4 -
小学生歌曲优美歌词摘抄VIP免费

 2024-12-01 4
2024-12-01 4 -
小学生必看的十部电影VIP免费

 2024-12-01 4
2024-12-01 4 -
小学生安全用电知识VIP免费

 2024-12-01 8
2024-12-01 8 -
小学教师精彩课堂教学用语教师言语道德集锦VIP免费

 2024-12-01 30
2024-12-01 30 -
小学1-6年级语文常识、名言名句、成语、谚语、歇后语大汇总VIP免费
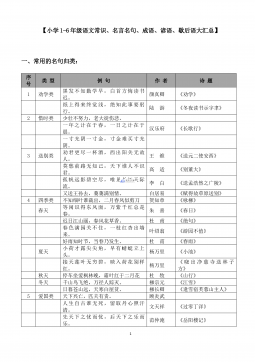
 2024-12-01 23
2024-12-01 23 -
五年级奥数期末测试卷VIP免费

 2024-12-01 17
2024-12-01 17 -
六年级计算题的复习与回顾练习VIP免费

 2024-12-01 9
2024-12-01 9 -
小学生礼仪常识VIP免费

 2024-12-01 13
2024-12-01 13
作者详情
相关内容
-

小学二年级上册上学期-部编版语文:寒号鸟 预习笔记
分类:幼儿/小学教育
时间:2025-08-25
标签:无
格式:PDF
价格:10 玖币
-

小学二年级上册上学期-部编版语文:古诗二首预习笔记
分类:幼儿/小学教育
时间:2025-08-25
标签:无
格式:PDF
价格:10 玖币
-

小学二年级上册上学期-部编版语文:第一课时预习笔记
分类:幼儿/小学教育
时间:2025-08-25
标签:无
格式:PDF
价格:10 玖币
-

小学二年级上册上学期-部编版语文:第三课时预习笔记
分类:幼儿/小学教育
时间:2025-08-25
标签:无
格式:PDF
价格:10 玖币
-

小学二年级上册上学期-部编版语文:第二课时预习笔记
分类:幼儿/小学教育
时间:2025-08-25
标签:无
格式:PDF
价格:10 玖币



 渝公网安备50010702506394
渝公网安备50010702506394
