矩阵理论与应用I-第三章4-对角化分解
VIP免费
2025-01-13
3
0
427.82KB
32 页
5.9玖币
侵权投诉
矩阵理论与应用I
第三章 矩阵分解
满秩分解
QR分解
Schur分解
对角化分解
谱分解
Jordan分解
第三章 矩阵分解
3.4 对角化分解
第三章 矩阵分解——对角化分解
定义3.4.1 单纯矩阵 若阶复方阵相似于对角阵,
即存在阶可逆矩阵使得
则矩阵称为可对角化矩阵或单纯矩
阵.
注1:单纯阵的定义式就是单纯阵的对角化分解式,
它实际上是Schur分解的一种特殊形式.
第三章 矩阵分解——对角化分解
定理3.4.1 设矩阵 的全部互异特征根为
,则以下命题等价:
(1)是单纯矩阵;
(2)有个线性无关的特征向量;
(3)特征值
的代数重数等于其几何
重数;
(4)
;
(5)最小多项式无重根.
第三章 矩阵分解——对角化分解
例3.4.1 设线性变换 在基 下的
矩阵为,即 ,其中
问:线性变换可否对角化.
若可对角化,试求满秩矩阵,使为对角阵
分析:线性变换可否对角化就等价于矩阵是否为
单纯矩阵.
第三章 矩阵分解——对角化分解
首先计算矩阵的特征多项式
方法一:又知 ,故的最小多项式为
.
由于无重根,故是单纯矩阵,即线性变换可
作对角化.
摘要:
展开>>
收起<<
矩阵理论与应用I第三章矩阵分解满秩分解QR分解Schur分解对角化分解谱分解Jordan分解第三章矩阵分解3.4对角化分解第三章矩阵分解——对角化分解定义3.4.1单纯矩阵若�阶复方阵�相似于对角阵Λ,即存在�阶可逆矩阵�使得�−1��=Λ则矩阵�称为可对角化矩阵ሺ或单纯矩ሻ阵.注1:单纯阵的定义式就是单纯阵的对角化分解式,它实际上是Schur分解的一种特殊形式.第三章矩阵分解——对角化分解定...
声明:本站为文档C2C交易模式,即用户上传的文档直接被用户下载,本站只是中间服务平台,本站所有文档下载所得的收益归上传人(含作者)所有。玖贝云文库仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对上载内容本身不做任何修改或编辑。若文档所含内容侵犯了您的版权或隐私,请立即通知玖贝云文库,我们立即给予删除!
相关推荐
-
安2-安3,26-21灌浆施工组织设计VIP免费

 2024-11-22 10
2024-11-22 10 -
XX水电站导流洞施工组织措施VIP免费

 2024-11-22 11
2024-11-22 11 -
xx公路施工组织设计VIP免费

 2024-11-22 12
2024-11-22 12 -
xx电站施工组织设计(投标阶段)VIP免费

 2024-11-22 12
2024-11-22 12 -
XXX土地开发整理项目投标文件 施工组织设计VIP免费

 2024-11-22 17
2024-11-22 17 -
pccp管穿河施工组织设计VIP免费

 2024-11-22 12
2024-11-22 12 -
110kv水利变电站施工组织设计VIP免费

 2024-11-22 13
2024-11-22 13 -
7套水电安装精选施工组织设计VIP免费

 2024-11-22 14
2024-11-22 14 -
×××供水工程施工组织设计VIP免费

 2024-11-22 18
2024-11-22 18 -
XX县城防堤施工组织设计1VIP免费

 2024-11-22 15
2024-11-22 15
分类:计算机
价格:5.9玖币
属性:32 页
大小:427.82KB
格式:PDF
时间:2025-01-13
作者详情
相关内容
-

电力工程资料:(一)目录
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-
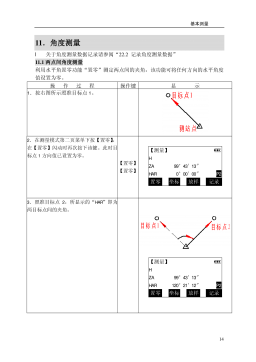
电力工程资料:(四)基本测量
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(六)数据记录
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(九)其他
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(完整word版)电力安全技术交底
分类:建筑/施工
时间:2025-06-07
标签:无
格式:DOCX
价格:10 玖币



 渝公网安备50010702506394
渝公网安备50010702506394
