模式识别(4)线性判别函数
模式识别第四章线性判别函数引言线性判别函数的基本概念Fisher线性判别函数感知准则函数最小平方误差准则函数多类问题内容第三章主要讲了类条件概率密度函数的估计参数估计方法最大似然估计贝叶斯估计非参数估计方法引言训练样本集样本分布的统计特征:概率密度函数决策规则:判别函数决策面方程基于样本的Bayes分类器:通过估计类条件概率密度函数,设计相应的判别函数引言MAXg1...g2gc...x1x2xna(x)分类器功能结构如果可以估计概率密度函数,则可以使用贝叶斯决策来最优的实现分类最一般情况下适用的“最优”分类器:错误率最小,对分类器设计在理论上有指导意义。获取统计...
相关推荐
-
安2-安3,26-21灌浆施工组织设计VIP免费

 2024-11-22 10
2024-11-22 10 -
XX水电站导流洞施工组织措施VIP免费

 2024-11-22 11
2024-11-22 11 -
xx公路施工组织设计VIP免费

 2024-11-22 12
2024-11-22 12 -
xx电站施工组织设计(投标阶段)VIP免费

 2024-11-22 12
2024-11-22 12 -
XXX土地开发整理项目投标文件 施工组织设计VIP免费

 2024-11-22 17
2024-11-22 17 -
pccp管穿河施工组织设计VIP免费

 2024-11-22 12
2024-11-22 12 -
110kv水利变电站施工组织设计VIP免费

 2024-11-22 13
2024-11-22 13 -
7套水电安装精选施工组织设计VIP免费

 2024-11-22 14
2024-11-22 14 -
×××供水工程施工组织设计VIP免费

 2024-11-22 18
2024-11-22 18 -
XX县城防堤施工组织设计1VIP免费

 2024-11-22 15
2024-11-22 15
作者详情
相关内容
-

电力工程资料:(一)目录
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-
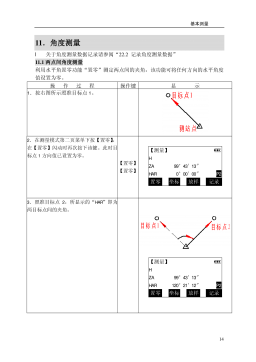
电力工程资料:(四)基本测量
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(六)数据记录
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(九)其他
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(完整word版)电力安全技术交底
分类:建筑/施工
时间:2025-06-07
标签:无
格式:DOCX
价格:10 玖币



 渝公网安备50010702506394
渝公网安备50010702506394
