035--算法常用面试题汇总
算法常用面试题汇总1.说一下什么是二分法?使用二分法时需要注意什么?如何用代码实现?二分法查找(BinarySearch)也称折半查找,是指当每次查询时,将数据分为前后两部分,再用中值和待搜索的值进行比较,如果搜索的值大于中值,则使用同样的方式(二分法)向后搜索,反之则向前搜索,直到搜索结束为止。二分法使用的时候需要注意:二分法只适用于有序的数据,也就是说,数据必须是从小到大,或是从大到小排序的。publicclassLesson7_4{publicstaticvoidmain(String[]args){//二分法查找int[]binaryNums={1,6,15,18,27,50};int...
相关推荐
-
安2-安3,26-21灌浆施工组织设计VIP免费

 2024-11-22 10
2024-11-22 10 -
XX水电站导流洞施工组织措施VIP免费

 2024-11-22 11
2024-11-22 11 -
xx公路施工组织设计VIP免费

 2024-11-22 12
2024-11-22 12 -
xx电站施工组织设计(投标阶段)VIP免费

 2024-11-22 12
2024-11-22 12 -
XXX土地开发整理项目投标文件 施工组织设计VIP免费

 2024-11-22 17
2024-11-22 17 -
pccp管穿河施工组织设计VIP免费

 2024-11-22 12
2024-11-22 12 -
110kv水利变电站施工组织设计VIP免费

 2024-11-22 13
2024-11-22 13 -
7套水电安装精选施工组织设计VIP免费

 2024-11-22 14
2024-11-22 14 -
×××供水工程施工组织设计VIP免费

 2024-11-22 18
2024-11-22 18 -
XX县城防堤施工组织设计1VIP免费

 2024-11-22 15
2024-11-22 15
作者详情
相关内容
-

电力工程资料:(一)目录
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-
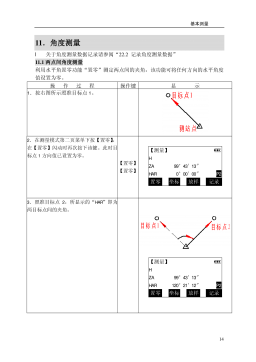
电力工程资料:(四)基本测量
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(六)数据记录
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(九)其他
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(完整word版)电力安全技术交底
分类:建筑/施工
时间:2025-06-07
标签:无
格式:DOCX
价格:10 玖币




 渝公网安备50010702506394
渝公网安备50010702506394
