Fast same-step forecast in SUTSE model and its theoretical properties Wataru Yoshida and Kei Hirose
Fastsame-stepforecastinSUTSEmodelanditstheoreticalpropertiesWataruYoshidaandKeiHiroseKyushuUniversityAbstractWeconsidertheproblemofforecastingmultivariatetimeseriesbyaSeeminglyUnrelatedTimeSeriesEquations(SUTSE)model.TheSUTSEmodelusuallyassumesthaterrorvariablesarecorrelated.Acrucialissueisthatthemo...
相关推荐
-
政治理论应知应会 100 题VIP免费

 2024-12-12 359
2024-12-12 359 -
2025年中央机关及其直属机构录用公务员考试 行政职业能力测验(地市级)(经典模考卷三)解析VIP免费

 2024-12-12 46
2024-12-12 46 -
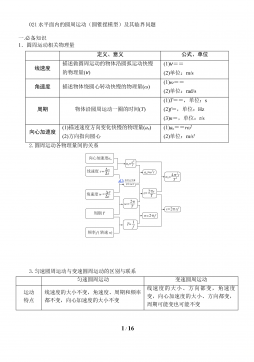
021水平面内的圆周运动(圆锥摆模型)及其临界问题 精讲精练-2022届高三物理一轮复习疑难突破微专题VIP免费
 2025-01-04 42
2025-01-04 42 -
21学位英语:从句考点真题VIP免费

 2025-04-08 4
2025-04-08 4 -
19学位英语:2010年阅读理解分析VIP免费

 2025-04-08 4
2025-04-08 4 -
[16] 学位英语:2007年阅读理解分析VIP免费

 2025-04-08 4
2025-04-08 4 -
[15] 学位英语:2006年阅读理解分析VIP免费

 2025-04-08 10
2025-04-08 10 -
[14] 学位英语:2005年阅读理解分析VIP免费

 2025-04-08 12
2025-04-08 12 -
[13] 学位英语:2004年阅读理解分析VIP免费

 2025-04-08 8
2025-04-08 8 -
[10] 学位英语:长难句拆分(二)VIP免费

 2025-04-08 10
2025-04-08 10
相关内容
-

[16] 学位英语:2007年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[15] 学位英语:2006年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[14] 学位英语:2005年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[13] 学位英语:2004年阅读理解分析
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币
-

[10] 学位英语:长难句拆分(二)
分类:高等教育
时间:2025-04-08
标签:无
格式:DOC
价格:5.9 玖币




 渝公网安备50010702506394
渝公网安备50010702506394
