模式识别(三概率密度函数的估计)
VIP免费
2025-01-13
2
0
1.01MB
64 页
5.9玖币
侵权投诉
模式识别
第三章 概率密度函数的估计
计算贝叶斯后验概率进行决策如何实现?
实现中有问题吗?能直接计算吗?
贝叶斯决策的实际使用
以第二章医生诊病为例:
先验概率未知,医生可大致估计
类条件概率密度呢?
只能通过已知的一些数据去估计
贝叶斯决策的实际使用
基于样本的两步贝叶斯决策
利用样本集估计 和
得到
和
然后将估计量带入贝叶斯决策规则中
得到决策结果
基于样本的两步贝叶斯决策
首先通过训练样本估计概率密度函数
先验概率估计 –训练样本分布情况/根据领域
知识认定
类条件概率密度估计难,本章重点
统计决策进行类别判定
基于样本的两步贝叶斯决策
训练样本有限,难以涵盖所有情况!
当训练样本无限多,基于样本的两步贝叶斯
决策可无限趋近第二章中的理论贝叶斯决策
当
基于样本的两步贝叶斯决策
由训练样本集估计总体概率密度的方法可分
为:
监督参数估计: 样本所属类别及类条件总体概
率密度函数形式已知,表征概率密度函数的某
些参数未知。
非监督参数估计: 已知总体概率密度函数形式
但未知样本所属类别,要求推断出概率密度函
数的某些参数。
非参数估计: 已知样本所属类别,未知总体概率
密度函数的形式,直接推断概率密度函数本身。
概率密度估计方法
统计量: 样本中包含着总体的信息,针对不
同要求构造出样本的某种函数,这种函数在
统计学中称统计量。
参数空间: 假设总体概率密度函数形式已知,
未知分布中的参数,的全部可容许值组成
的集合称为参数空间,记为
参数估计的基本概念
点估计:点估计问题就是要构造一个统计量
作为参数的估计
。
估计量:
被称为的估计量。
估计值:如果
是属于类别的样
本的观察值,代入统计量d就得到对于第i类
的
的具体数值,这一数值被称为的估计值。
参数估计的基本概念
摘要:
展开>>
收起<<
模式识别第三章概率密度函数的估计计算贝叶斯后验概率进行决策如何实现?实现中有问题吗?能直接计算吗?贝叶斯决策的实际使用������(��ȁ������)=�(������ȁ��)������(��)σ�=���(������ห��)������(��)以第二章医生诊病为例:������&#...
声明:本站为文档C2C交易模式,即用户上传的文档直接被用户下载,本站只是中间服务平台,本站所有文档下载所得的收益归上传人(含作者)所有。玖贝云文库仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对上载内容本身不做任何修改或编辑。若文档所含内容侵犯了您的版权或隐私,请立即通知玖贝云文库,我们立即给予删除!
相关推荐
-
安2-安3,26-21灌浆施工组织设计VIP免费

 2024-11-22 10
2024-11-22 10 -
XX水电站导流洞施工组织措施VIP免费

 2024-11-22 11
2024-11-22 11 -
xx公路施工组织设计VIP免费

 2024-11-22 12
2024-11-22 12 -
xx电站施工组织设计(投标阶段)VIP免费

 2024-11-22 12
2024-11-22 12 -
XXX土地开发整理项目投标文件 施工组织设计VIP免费

 2024-11-22 17
2024-11-22 17 -
pccp管穿河施工组织设计VIP免费

 2024-11-22 12
2024-11-22 12 -
110kv水利变电站施工组织设计VIP免费

 2024-11-22 13
2024-11-22 13 -
7套水电安装精选施工组织设计VIP免费

 2024-11-22 14
2024-11-22 14 -
×××供水工程施工组织设计VIP免费

 2024-11-22 18
2024-11-22 18 -
XX县城防堤施工组织设计1VIP免费

 2024-11-22 15
2024-11-22 15
分类:计算机
价格:5.9玖币
属性:64 页
大小:1.01MB
格式:PDF
时间:2025-01-13
作者详情
相关内容
-

电力工程资料:(一)目录
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-
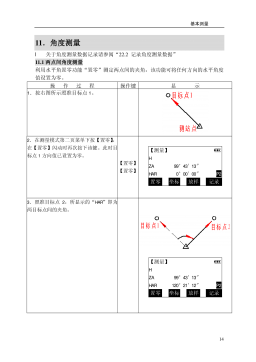
电力工程资料:(四)基本测量
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(六)数据记录
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(九)其他
分类:建筑/施工
时间:2025-06-07
标签:无
格式:PDF
价格:10 玖币
-

电力工程资料:(完整word版)电力安全技术交底
分类:建筑/施工
时间:2025-06-07
标签:无
格式:DOCX
价格:10 玖币



 渝公网安备50010702506394
渝公网安备50010702506394
